2023. 3. 7. 02:50ㆍ알고리즘/개념
아래에 3개의 문제가 있습니다.
1. 디펜스 게임
https://school.programmers.co.kr/learn/courses/30/lessons/142085
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
2. 시소 짝꿍
https://school.programmers.co.kr/learn/courses/30/lessons/152996
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
3. 입국 심사
https://school.programmers.co.kr/learn/courses/30/lessons/43238
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
다른 방식의 풀이가 있겠지만 저는 이분탐색을 사용하여 위 3개의 문제를 해결하였습니다.
자세한 풀이는 저작권 이슈가 생길 수 있으므로 다루지 않겠습니다.
먼저 이진탐색을 공부하고
이분 탐색이 3문제에 어떻게 적용 가능한지만 짧게 다루겠습니다.
이분 탐색이 뭐예요? What?
데이터의 범위를 절반씩 줄여가며 데이터를 탐색하는 방법
이분 탐색은 언제 써요? When?
최댓값 or 최솟값을 구해야 하는 경우 한번 생각해 볼 만합니다.
문제에 주어진 입력값들의 범위가 터무니없이 클 때,
Int를 벗어난 많은 경우 풀이 방법으로 고려해 볼 만합니다..
이분 탐색을 왜 써요? Why?
최대 최소를 미리 x라 가정하고 결과에 따라 x보다 클 수 있는지 작아도 되는지를 따지면
최대 최소 문제가 결정 문제로 바뀌게 됩니다.
범위가 너무 커 반복문을 2번 돌리면 분명 시간초과가 날 것이고 연산 횟수가 10억은 가볍게 넘어갈 것입니다.
이럴 때 이진탐색은 시간복잡도를 O( logN )으로 낮춰 많은 경우 시간을 초과하지 않고 효율성을 통과할 수 있게 만듭니다.
이분 탐색은 어떻게 써요? How?
2번 문제 디펜스 게임을 잠깐 볼까요??
준호가 처음 가지고 있는 병사의 수 n, 사용 가능한 무적권의 횟수 k, 매 라운드마다 공격해 오는 적의 수가 순서대로 담긴 정수 배열 enemy가 매개변수로 주어집니다. 준호가 몇 라운드까지 막을 수 있는지 return 하도록 solution 함수를 완성해 주세요.
우리가 구해야 하는 것은 몇 라운드까지 막을 수 있는지예요.
이 문제를 만약 1번 라운드부터 하나씩 증가하며 가능한지 아닌지를 판별한다면 가능하긴 하지만
데이터가 크다면... 결과는 좋지 않겠죠.
그래서 조금 다르게 생각해 보는 겁니다.
만약 준호가 30라운드까지 막을 수 있어라고 가정한다면 30라운드까지는 분명히 막을 수 있다는 결과가 나와야 하겠죠.
그런데 만약 막지 못한다면?
이때는 '30라운드는 막을 수 없으니까 답이 30라운드보다는 작겠구나'라고 알 수 있겠죠.
만약 막을 수 있다면 이 경우는 30라운드는 막을 수 있으면 30라운드 보다 큰 라운드는 막을 수 있을까? 하고 더 큰 값이 가능한지 확인해 보러 가는 겁니다.
여기서 이분 탐색이 나오게 됩니다.
하나 더 예를 들어 입국심사 문제를 보겠습니다.
입국심사를 기다리는 사람 수 n, 각 심사관이 한 명을 심사하는 데 걸리는 시간이 담긴 배열 times가 매개변수로 주어질 때, 모든 사람이 심사를 받는 데 걸리는 시간의 최솟값을 return 하도록 solution 함수를 작성해 주세요.
우리는 모든 사람이 심사를 받기 위한 시간의 최솟값을 구해야 합니다.
앞에서는 준호가 막을 수 있는 라운드의 최댓값을 구해야 했습니다.
만약 모든 사람의 심사를 받을 수 있는 시간이 50분이면 50분에는 모든 사람이 심사를 받고 끝나겠죠??
50분에 심사해야 하는 사람이 남았다면 50분은 모든 사람을 처리하기엔 부족한 시간이므로 답은 50분 보다 더 커야 합니다.
만약 50분까지 심사를 할 수 있는 사람이 전체 기다리는 사람보다 많다면 50분에는 전부 처리하고 남는다는 말이므로 50분보다 더 적을 수 있는지 확인해야 합니다.
위의 두 가지 문제 예를 통해 무엇이고 왜 쓰고 언제 쓰는지를 파악해 보았습니다.
이제 이분탐색의 기본적인 코드, upper bound , lower bound를 구현해 보겠습니다
1. 이분탐색
2. Lower Bound
3. Upper Bound
1. 이분탐색
기본적인 이분 탐색의 과정을 다시 정리해 보겠습니다.
아래의 그림에서 7을 찾는 과정을 보겠습니다.




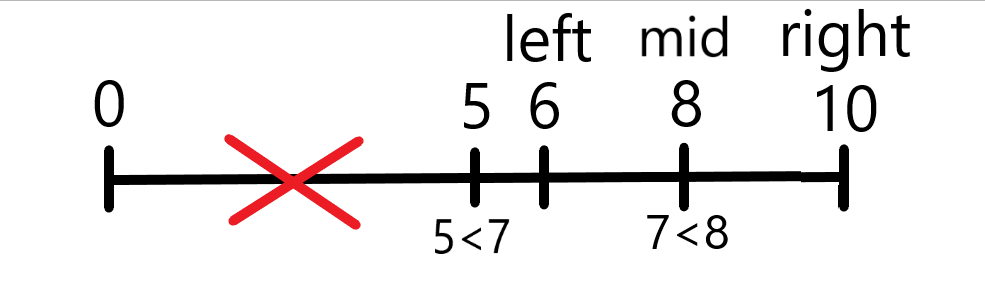
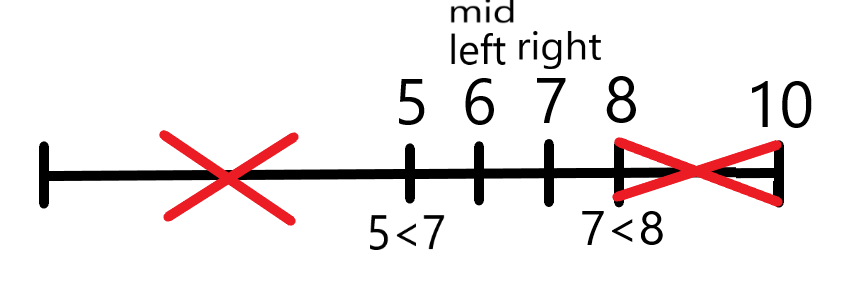
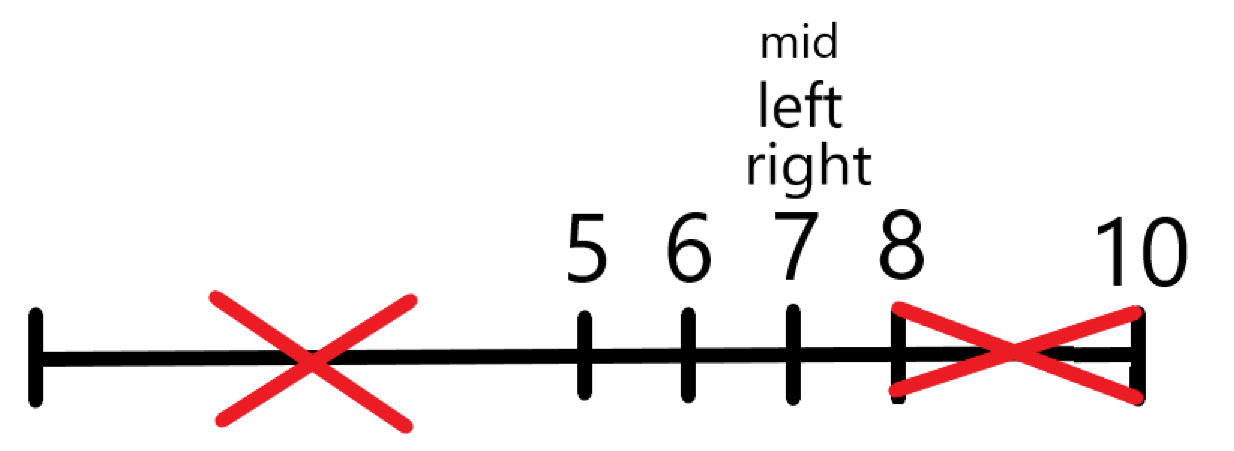
각 영역을 절반씩 줄여 나가고 있습니다.
탈출 조건은 두 가지로 target을 찾거나 다 돌리고 left 가 right를 넘어서는 순간 탈출합니다.
위의 그림을
코드는 아래와 같습니다.
fun binarySearch(arr: IntArray, target: Int) : Int {
var left = 0
var right = arr.size-1
while(left<=right) {
val mid = (left+right)/2
if(arr[mid] == target) return mid
else if(arr[mid] > target) right = mid-1
else left = mid+1
}
return -1
}
위의 코드는 우리가 찾는 target이 배열에 있는지 없는지 알 수 있게 해 줍니다.
정확히 값이 맞아야 반환하죠.
하지만 배열 안에 언제 최소로 얻냐 언제 최대를 얻냐를 물어본다면 약간은 달라지게 됩니다.
이제 upper bound와 lower bound 가 어떻게 나오는지 알아보겠습니다.
2. Lower Bound
그림이 하나 있습니다.
왼쪽에는 Lower bound 오른쪽에는 Upper bound라고 적혀있습니다.
그림을 보고 대략적으로 이런 것이구나 느낌이 오시나요??

Lower Bound는 특정 값의 시작 위치를 알려줍니다.
어떤 값이나 조건에 맞는 경우는 여러 개가 있을 수 있습니다.
만약 가능한 경우 최소 언제이냐,
밥을 최소 몇 번 먹어야 하냐
언제부터 가야 가능하냐
심사가 최소 언제 끝나냐 등 이렇게 말하면
특정 값이 포함되는 경우의 시작 위치를 구해 알 수 있습니다.
코드는 아래와 같습니다.
fun lowerBound(arr: IntArray, target: Int) : Int {
var left = 0
var right = arr.size
while(left<right) {
val mid = (left+right)/2
if(arr[mid]<target) left = mid+1
else right = mid
}
return right
}
right 가 이분탐색과는 다르게 arr.size입니다.
왜냐하면 찾는 값이 배열의 가장 큰 값보다 큰 경우도 배열에는 없기 때문에
'배열 안에는 없어. 입력된 배열 끝의 가장 큰 값보다 크기 때문에 네가 찾는 값은 배열의 끝에부터 있을 수도 있어!' 생각해야 하기 때문입니다.
if 문을 보면 target 보다 작을 때 왼쪽 검색 index 값을 mid +1 하고 있습니다.
lower bound는 언제부터 가능하냐 이 말과 같기 때문에 아예 작을 때는 불가능하므로 필요가 없습니다.
반대로 크거나 같을 때는 가능하기 때문에 오른쪽 끝을 계속 mid로 변경하는 것입니다.
오른쪽 끝에는 가능한 경우가, 왼쪽에 안 되는 경우를 버리면서 찾으면
결국 가장 처음 가능한 경우 왼쪽 오른쪽으로 left와 right 가 찾게 되고 둘이 만나 결과를 반환합니다.
upper bound도 마찬가지입니다.
3. upper bound
upper bound는 특정 값보다 처음으로 큰 값을 갖는 경우를 찾게 해 줍니다.
경계 밖의 시작이 언제인지를 알려주기 때문에 경계 안의 최대도 알 수 있게 해 줍니다.
최대 얼마만큼 먹을 수 있어?
최대 얼마나 갈 수 있어?
어디까지 막을 수 있어?
등의 최대 언제 가능한지는 처음으로 큰 값 바로 앞에 값입니다.
아래 코드가 있습니다.
fun upperBound(arr: IntArray, target: Int): Int {
var left= 0
var right = arr.size
while(left<right) {
val mid = (left+right)/2
if(arr[mid] <= target) left = mid+1
else right = mid
}
return right
}
upper bound도 arr.size 사이즈가 가장 끝입니다.
upperbound를 이용해 값을 구하면 최대 언제까지 가능한지 알 수 있게 합니다.
왼쪽에 가능한 경우를 점점 줄이면 마지막 가능한 경우의 끝에 옵니다.
오른쪽은 불가능한 경우를 버리면서 오게 되면 최대 가능한 경우 뒤로 옵니다.
그 사이에 최대 가능한 경계, 처음으로 초과하는 값이 나오는 upper bound가 있습니다.
upper bound는 처음으로 큰 값이 나오는 때를 알려줍니다.
그러므로 처음으로 큰 값이 나오는 값의 -1 한 값이 조건을 만족하는 최대 가능한 경우가 됩니다.
이렇게 문제에서 응용이 가능합니다.
'알고리즘 > 개념' 카테고리의 다른 글
| BackTracking 백트래킹 설명 및 문제 예시 (0) | 2023.03.14 |
|---|---|
| 다익스트라(Dijkstra) 알고리즘 - Kotlin (0) | 2023.03.07 |
| DFS & BFS ( Kotlin ) (0) | 2023.03.07 |
| 플로이드 와샬 ( Floyd Warshall ) 알고리즘 - (Kotlin) (0) | 2023.03.05 |
| 크루스칼 알고리즘 & Union Find 알고리즘 ( 최소 신장 트리 , Kotlin ) (0) | 2023.03.02 |