2023. 3. 7. 23:29ㆍ알고리즘/개념
다익스트라 알고리즘
다익스트라 알고리즘은 무엇인가요??
다익스트라 알고리즘은 대표적인 최단 경로 탐색 알고리즘입니다.
하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 알려줍니다.
언제 사용하나요??
말했다시피 목적지로 가기 위한 최단 경로를 구하기 위해 사용합니다.
특징은 음의 간선이 포함되지 않아 현실 세계에 데이터를 가지고 사용하기 좋습니다.
그래서 인공위성 GPS 내비게이션 등 다양한 곳에서 사용합니다.
문제가 그래프로 나와 최단 경로를 구해야 한다면 생각해 볼 만합니다.
왜 사용하나요??
다익스트라 알고리즘은 다이내믹 프로그래밍입니다.
최단 경로로 가기 위해서는 가는 길도 최단 경로여야 합니다.
이전까지의 최단 경로를 저장해 구하려는 최단 경로를 구하기 때문에 작은 문제를 가지고 큰 문제를 해결하는 다이내믹 프로그래밍이라고 할 수 있습니다.
어떻게 사용하나요??
기본 구형 과정
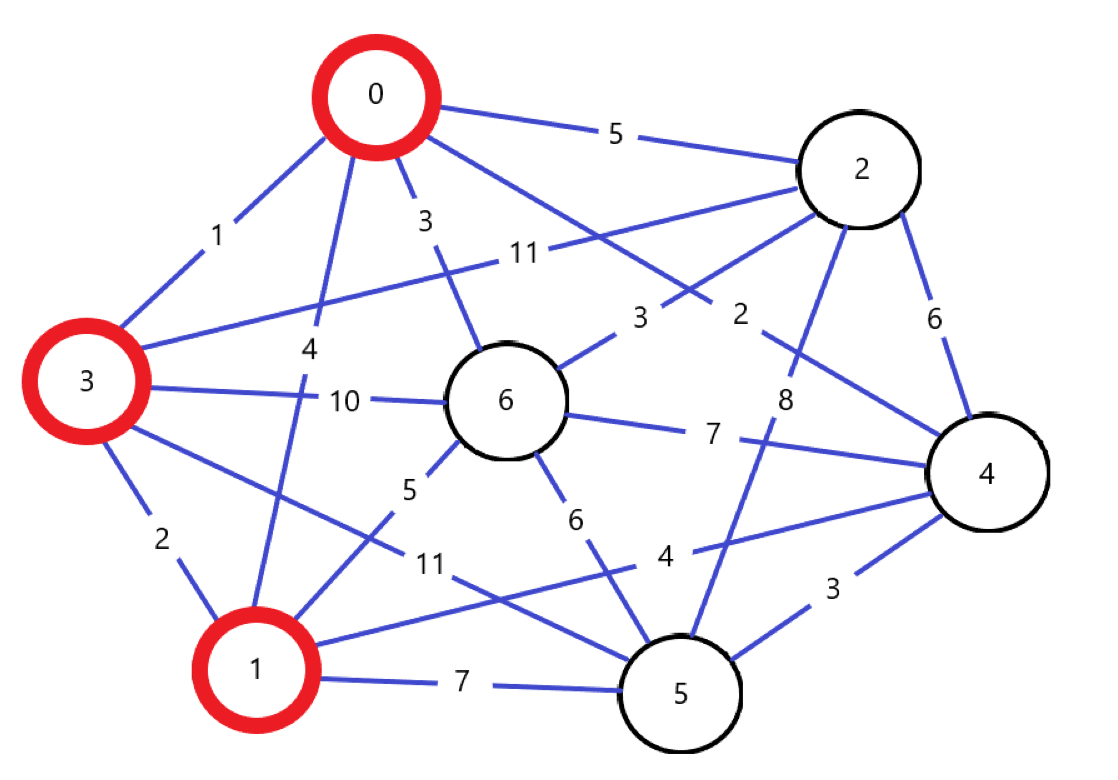
다익스트라 알고리즘의 기본 구현 과정을 먼저 소개합니다. 아래에 그래프가 있습니다.

먼저 각 그래프에서 갈 수 있는 인접 노드의 가중치 값을 정리해서 배열로 만들어보겠습니다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 0 | 0 | 4 | 5 | 1 | 2 | INF | 3 |
| 1 | 4 | 0 | INF | 2 | 4 | 7 | 5 |
| 2 | 5 | INF | 0 | 11 | 6 | 8 | 3 |
| 3 | 1 | 2 | 11 | 0 | INF | 11 | 10 |
| 4 | 2 | 4 | 6 | INF | 0 | 3 | 7 |
| 5 | INF | 7 | 8 | 11 | 3 | 0 | 6 |
| 6 | 3 | 5 | 3 | 10 | 7 | 6 | 0 |
이제 시작 노드에서 다른 모든 노드까지의 최단 거리를 갱신하기 위해 먼저 출발하는 시작 노드를 선택합니다.
3번 노드를 선택하겠습니다.
3번 정점에서 다른 정점으로 갈 수 있는 초기 값이 있습니다. 위의 배열에서 3번 노드를 가져왔습니다.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 1 | 2 | 11 | 0 | INF | 11 | 10 |
또한 방문체크를 위한 Visited 배열을 만들겠습니다.
visited 배열입니다. 처음 3번 노드 시작을 위해 3번 노드 방문 표시를 합니다.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| visited[i] | false | false | false | true | false | false | false |
3번 배열에서 방문하지 않은 노드 중 가장 거리가 짧은 노드를 선택합니다.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 1 | 2 | 11 | 0 | INF | 11 | 10 |
가장 짧은 노드는 index = 0 일 때, 가중치 1이 가장 작은 값을 가집니다.
0번 노드를 거쳐서 가는 경우로 다른 노드를 모두 확인해 봅니다.

3번에서 0을 거쳐 1로 가면 1+4 = 5입니다. 3번에서 1로 직행하면 2입니다. 2가 더 적으므로 갱신하지 않습니다.
3번에서 0을 거쳐 2로 가면 1+5 = 6입니다. 3번에서 2로 직행하면 11입니다. 6이 더 적으므로 갱신합니다.
3번에서 0을 거쳐 4로 가면 1+2 = 3입니다. 3번에서 4로 직행은 없어 INF 값이었습니다. 고로 갱신합니다.
3번에서 0을 거쳐 5로 한 번에 갈 수 없습니다. 갱신하지 않습니다.
3번에서 0을 거쳐 6으로 가면 1+3 = 4입니다. 3번에서 6으로 직행하면 10입니다. 4가 더 적으므로 갱신합니다.
갱신된 배열은 다음과 같습니다.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| visited[i] | true | false | false | true | false | false | false |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 1 | 2 | 11 => 6 | 0 | INF => 3 | 11 | 10 => 4 |
위의 visited 배열에서 방문하지 않았으며 3번 노드의 거리 배열에서 값이 가장 작은 노드를 확인합니다.
가장 값이 작은 노드는 1입니다.
visited 배열을 갱신해 주고
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| visited[i] | true | true | false | true | false | false | false |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 1 | 2 | 6 | 0 | 3 | 11 => 9 | 4 |
이제 다시 3번에서 1번을 거쳐 가는 방문하지 않은 모든 노드를 확인합니다.
3번에서 1번을 거쳐 2번을 거쳐 갈 수 없습니다. 갱신하지 않습니다.
3번에서 1번을 거쳐 4번으로 가면 6입니다. 기존에 3번에서 4번으로 가는 값은 3입니다. 갱신하지 않습니다.
3번에서 1번을 거쳐 5번으로 가면 9입니다. 기존에 3번에서 5번으로 가는 값은 11입니다. 갱신합니다.
3번에서 1번을 거쳐 6번으로 가면 7입니다. 기존에 3번에서 6번으로 가는 값은 4입니다. 갱신하지 않습니다.
갱신된 배열입니다.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 1 | 2 | 6 | 0 | 3 | 9 | 4 |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| visited[i] | true | true | false | true | false | false | false |
이제 위와 동일한 방식으로 방문하지 않았으며 그중 가장 작은 정점을 찾습니다.
정점은 4번 정점입니다.
visited 배열을 갱신 확인합니다.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| visited[i] | true | true | false | true | true | false | false |

| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 1 | 2 | 5 | 0 | 3 | 9 => 6 | 4 |
3번에서 4번을 거쳐 2번으로 가면 9입니다. 기존에 3번에서 2번으로 가는 값은 5입니다. 갱신하지 않습니다.
3번에서 4번을 거쳐 5번으로 가면 6입니다. 기존에 3번에서 5번으로 가는 값은 9입니다. 갱신합니다.
3번에서 4번을 거쳐 6번으로 가면 10입니다. 기존에 3번에서 6번으로 가는 값은 4입니다. 갱신하지 않습니다.
갱신된 3번 정점의 배열은 다음과 같습니다.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 1 | 2 | 6 | 0 | 3 | 6 | 4 |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| visited[i] | true | true | false | true | true | false | false |
다시 방문하지 않은 것 중 가장 적은 값의 정점을 찾습니다.
6번 정점입니다.
visited 배열을 갱신합니다.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| visited[i] | true | true | false | true | true | false | true |

| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 1 | 2 | 6 | 0 | 3 | 6 | 4 |
3번 정점에서 6번을 거쳐 2번으로 가면 7입니다. 기존에 값은 4입니다. 갱신하지 않습니다.
3번 정점에서 6번을 거쳐 5번으로 가면 10입니다. 기존에 값은 6입니다. 갱신하지 않습니다.
또 찾습니다. 그러면 2번 정점임을 알 수 있습니다.
visited 배열을 갱신합니다.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| visited[i] | true | true | true | true | true | false | true |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 1 | 2 | 6 | 0 | 3 | 6 | 4 |

3번 정점에서 2번을 거쳐 5번으로 가면 14입니다. 기존에 값은 6입니다. 갱신하지 않습니다.
이제 마지막으로 5번 정점 하나만 남았습니다.

결과는 다음과 같이 나오게 됩니다.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 1 | 2 | 6 | 0 | 3 | 6 | 4 |
위의 과정을 코드로 옮기면 아래와 같습니다. 다익스트라의 기본적이 코드입니다. 시간 복잡도는 O(N^2)을 가집니다.
코드


val arr = Array<IntArray>(7) { IntArray(7) }
fun main(){
arr[0] = intArrayOf(0,4,5,1,2, 10000000,3)
arr[1] = intArrayOf(4,0,10000000,2,4,7,5)
arr[2] = intArrayOf(5, 10000000,0,11,6,8,3)
arr[3] = intArrayOf(1,2,11,0,10000000,11,10)
arr[4] = intArrayOf(2,4,6,10000000,0,3,7)
arr[5] = intArrayOf(10000000,7,8,11,3,0,6)
arr[6] = intArrayOf(3,5,3,10,7,6,0)
val result = dikjstra(3)
println(result.toList())
}
fun dikjstra(start: Int): IntArray {
val distance = arr[start]
val visited = BooleanArray(distance.size){ false }
visited[start] = true
repeat(distance.lastIndex-1) {
val minIndex = getMinIndex(distance,visited)
visited[minIndex] = true
arr[minIndex].forEachIndexed { i, cost ->
if(!visited[i] && (distance[minIndex] + cost < distance[i])){
distance[i] = distance[minIndex] + cost
}
}
}
return distance
}
fun getMinIndex(arr: IntArray, visited: BooleanArray) : Int {
var min = 10000000
var index = 0
arr.forEachIndexed { i, cost ->
if(cost<min && !visited[i]) {
min = cost
index = i
}
}
return index
}O(N * logN)의 방식 - Priority Queue, Pair
Priority Queue, Pair <Int, Int>를 이용한 다익스트라 알고리즘

val graph = Array(7) { mutableListOf<Pair<Int,Int>>() }
fun main(){
graph[0].add(Pair(1,4))
graph[0].add(Pair(2,5))
graph[0].add(Pair(3,1))
graph[0].add(Pair(4,2))
graph[0].add(Pair(6,3))
graph[1].add(Pair(3,2))
graph[1].add(Pair(0,4))
graph[1].add(Pair(4,4))
graph[1].add(Pair(5,7))
graph[1].add(Pair(6,5))
graph[2].add(Pair(0,5))
graph[2].add(Pair(3,11))
graph[2].add(Pair(4,6))
graph[2].add(Pair(5,8))
graph[2].add(Pair(6,3))
graph[3].add(Pair(0,1))
graph[3].add(Pair(1,2))
graph[3].add(Pair(2,11))
graph[3].add(Pair(5,11))
graph[3].add(Pair(6,10))
graph[4].add(Pair(2,6))
graph[4].add(Pair(0,2))
graph[4].add(Pair(5,3))
graph[4].add(Pair(1,4))
graph[4].add(Pair(5,3))
graph[5].add(Pair(1,7))
graph[5].add(Pair(2,8))
graph[5].add(Pair(3,11))
graph[5].add(Pair(4,3))
graph[5].add(Pair(6,6))
graph[6].add(Pair(0,3))
graph[6].add(Pair(1,5))
graph[6].add(Pair(2,3))
graph[6].add(Pair(4,7))
graph[6].add(Pair(5,4))
val result = dijkstra(3)
println(result.toList())
}
fun dijkstra(node: Int): IntArray {
val distance = IntArray(graph.size){ 100000000 }
val pQueue = PriorityQueue<Pair<Int, Int>>{ p1, p2 ->
p1.second.compareTo(p2.second)
}
distance[node] = 0
pQueue.add(Pair(node, 0))
while(pQueue.isNotEmpty()) {
val (currentIndex,currentCost) = pQueue.poll()
if(distance[currentIndex] < currentCost) continue
graph[currentIndex].forEach { next ->
val nextIndex = next.first
val nextCost = currentCost + next.second
if(nextCost < distance[nextIndex]) {
distance[nextIndex] = nextCost
pQueue.add(Pair(nextIndex, nextCost))
}
}
}
return distance
}우선순위 큐를 이용하여 다익스트라 기본 구현의 getMinIndex() 과정을 빠르게 처리하는 방법이다. 위와 같은 방법으로 하면 O(N*logN)의 시간복잡도로 구현할 수 있다. Pair를 이용하여 그래프를 구성하고 우선순위큐를 선언할 때 거리가 작은 경우로 우선순위를 정하기 위해 p1.second.compareTo(p2.second)를 사용하여 거리 최소힙을 구현한다. 그리고 q가 비어있지 않을 때까지 반복하며 거리 배열에 노드를 거쳐가는 거리와 바로 가는 값을 비교하여 만약 이미 바로 가는 값보다 작은 값이 있다면 처리가 된 것이므로 continue 하고 그게 아니라면 중간까지 거리의 최솟값 + 중간부터 다른 노드까지의 결과를 더해 확인한다.
초기 priority Queue에는 시작 노드가 들어있다.

초기 시작 노드 자신이 갈 수 있는 graph[currentIndex]를 forEach를 통해 확인한다. 이때 값은 0,1,2,5,6 5개의 노드를 반복문을 통해 확인하는데 distance가 초기값으로 10000000 아주 큰 값이 들어있기 때문에 처음에는 무조건 distance [currentIndex] 값보다 currentCost + nextCost 값이 작을 수밖에 없다. 자기 자신 값 0에 갈 수 있는 노드 값들을 더하기 때문에 시작은 일단 이렇게 시작한다.
다음 priority Queue에서 하나 poll 해가지고 가지고 온다. 이제부터 노드를 중간에 거쳐가면서 거리를 확인하는 과정을 시작한다. priority Queue를 통해 poll하기 때문에 3번 노드가 갈 수 있는 노드들 중 가장 cost가 작은 노드가 먼저 나온다.

위의 그림을 보면 poll 해서 가져온 0번 노드를 가지고 forEach를 통해 갈 수 있는 노드들을 확인한다.
0번까지 거리 값이 currentCost이고 0번이 갈 수 있는 값은 nextCost이다. 만약 currentCost+nextCost가 3번 노드에서 가는 값보다 적다면 distance[nextIndex] 값을 더 작은 값 currentCost+nextCost 값으로 재할당한다. 그리고 priority Queue에 갱신하는 노드의 Pair를 삽입한다. 만약 2번 노드라고 생각해 보면 2번까지는 6이 현재 11보다 더 적으므로 distance[2]을 6으로 갱신하고 priority queue에 Pair(2,6)을 삽입한다. 그러면 이미 존재하는 Pair(2,11)보다 앞의 값을 가지고 2까지는 최소의 값을 가지게 처리한다.
위의 과정을 계속 반복하여 최소 값을 가진 노드를 거쳐 다음 노드도 최소를 선택해 모든 노드로 가는 가장 적은 cost 값을 알게 된다. 이상으로 다익스트라 알고리즘 정리였다.
'알고리즘 > 개념' 카테고리의 다른 글
| 정렬 알고리즘 정리 코틀린 (0) | 2023.05.03 |
|---|---|
| BackTracking 백트래킹 설명 및 문제 예시 (0) | 2023.03.14 |
| DFS & BFS ( Kotlin ) (0) | 2023.03.07 |
| 이분탐색 파라매트릭 서치 알고리즘 ( Kotlin ) (0) | 2023.03.07 |
| 플로이드 와샬 ( Floyd Warshall ) 알고리즘 - (Kotlin) (0) | 2023.03.05 |