2023. 3. 5. 22:00ㆍ알고리즘/개념
플로이드 와샬 알고리즘 - 최단 거리 알고리즘 (2)

최단 거리 알고리즘 중에 하나인 플로이드 와샬 알고리즘을 알아보겠다. 그래프를 보면 1번에서 5번으로 가기 위한 방법은 아주 많은데 플로이드 와샬 알고리즘은 어떻게 가장 짧은 거리를 알 수 있을까?
그래프 초기화
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 0 | 5 | 9 | 14 | many | many |
| 2 | 5 | 0 | 36 | many | 47 | many |
| 3 | 9 | 36 | 0 | 22 | 55 | 88 |
| 4 | 14 | many | 22 | 0 | many | 31 |
| 5 | many | 47 | 55 | many | 0 | 11 |
| 6 | many | many | 88 | 31 | 11 | 0 |
먼저 그래프를 초기화한다. 그림은 무방향인데 방향이 있어도 똑같다. 방향이 있다면 없는 방향은 그냥 many라고 생각하고 큰 수를 넣어주든가 하자. 다만 +의 영향으로 Int.Max value를 하게 되면 int 범위를 넘어가서 원하는 답이 안 나올 수 있음에 주의하자.
플로이드 와샬의 기본적인 이해

위의 반복 과정을 보고 생각하면 이해하기 더 쉽다. 첫 번째로 먼저 자기 자신을 중간에 들리면 시작부터 종점까지 직행이 된다. 시작과 중간이 같으면 중간에 처리하지 않고 신경 쓰지 않는다.
두 번째에

정점 2에서 출발하여 중간에 정점 1을 들렸다가 정점 3으로 가는 거리는 14인데 직행이 36이다. 돌아가는 게 더 빠르다.
하나 더 보면

그래프를 초기화했을 때 시작 2에서 4로 가는 방법은 무수히 많아 값을 정하지 못했었다. 하지만 1을 들려서 2에서 4로 가는 방법이 생겼으므로 거리 배열을 돌아가는 값 19로 값을 할당할 수 있게 된다. 현재까지 2에서 4로 가는 가장 빠른 값은 19가 된다.

이러한 경우는 정점 2에서 1을 중간 지점으로 갔다 5로 가는 경우인데 정점 1에서 정점 5로 갈 수 있는 방법은 너무 많다. 그래서 돌아가면 10000000 many값에 5를 더한 값이 나온다. Many에 5 더해도 Many라고 생각할 수 있으므로 이런 경우는 당연히 그냥 넘어간다. 직행이 무조건 빠르다.

이런 경우도 있다. 정점 4에서 시작해 1을 들려서 5로 가는 경우인데 보면 4에서 1로는 직행이 있는데 1에서 5로 갈 수 있는 방법이 아주 많다. 그래서 돌아가도 10000014라는 큰 수가 나온다. 그리고 4에서 5로 한 번에 갈 수 있는 방법도 없다. 직행도 아주 많다. 결국 돌아가나 직행하나 둘 다 Many라고 생각하면 된다. 이런 경우는 distance 배열에 직행하는 10000000 값이 들어가게 된다. 그냥 Many 그대로 할당한다는 소리다.
한 번의 결과는 아래와 같이 반복된다.

중간의 거점을 먼저 고정한다. 그리고 시작을 고정하고 마지막에 도착하는 곳을 반복하면서 확인한다.
이러한 사이클을 반복하면서 모든 정점을 확인한다.
그림으로 보면
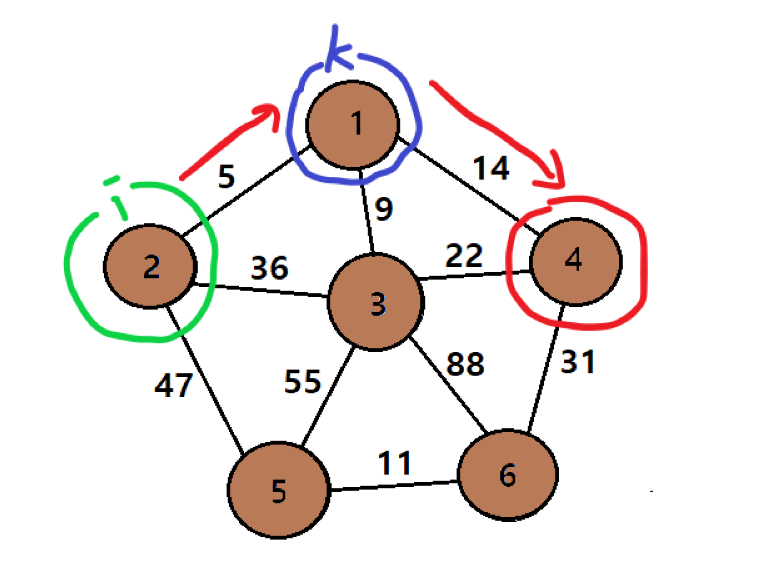
정점 2에서 정점 1을 들려 4로 가는 값은 19입니다. 이때 distance [2][4] = 19로 갱신된다.
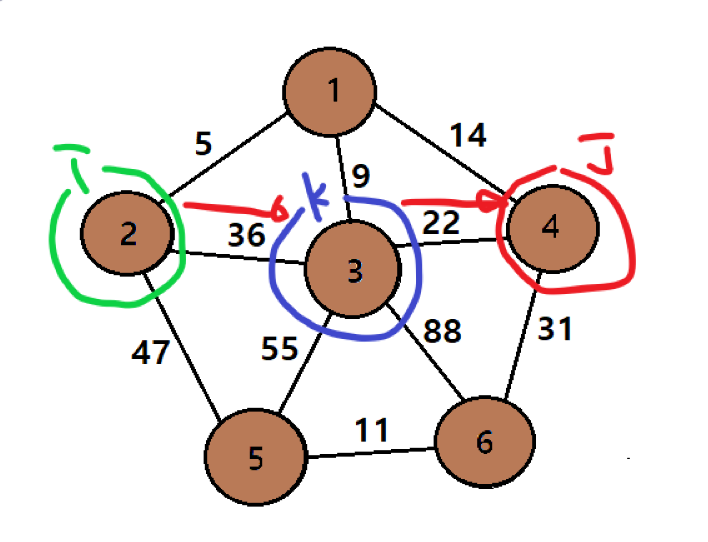
중간에 들리는 정점 k가 3이고 i가 2일 때 4로 가는 거리 값은 36+22로 58입니다. 이미 2에서 4로 가는 거리 값은 더 작은 19가 할당되어 있다. 그러므로 갱신하지 않는다.
이와 같이 모든 중간 정점을 두고 출발 정점 도착 정점을 반복함으로 모든 정점으로부터 모든 정점으로 가는 거리의 최솟값을 알 수 있다.
코드
fun main(args: Array<String>) {
val graph = arrayOf(
intArrayOf(0,5,9,14,10000000,10000000),
intArrayOf(5,0,36,10000000,47,10000000),
intArrayOf(9,36,0,22,55,88),
intArrayOf(14,10000000,22,0,10000000,31),
intArrayOf(10000000,47,55,10000000,0,11),
intArrayOf(10000000,10000000,88,31,11,0)
)
val result = floydWarshall(graph)
result.forEach {
println(it.toList())
}
}
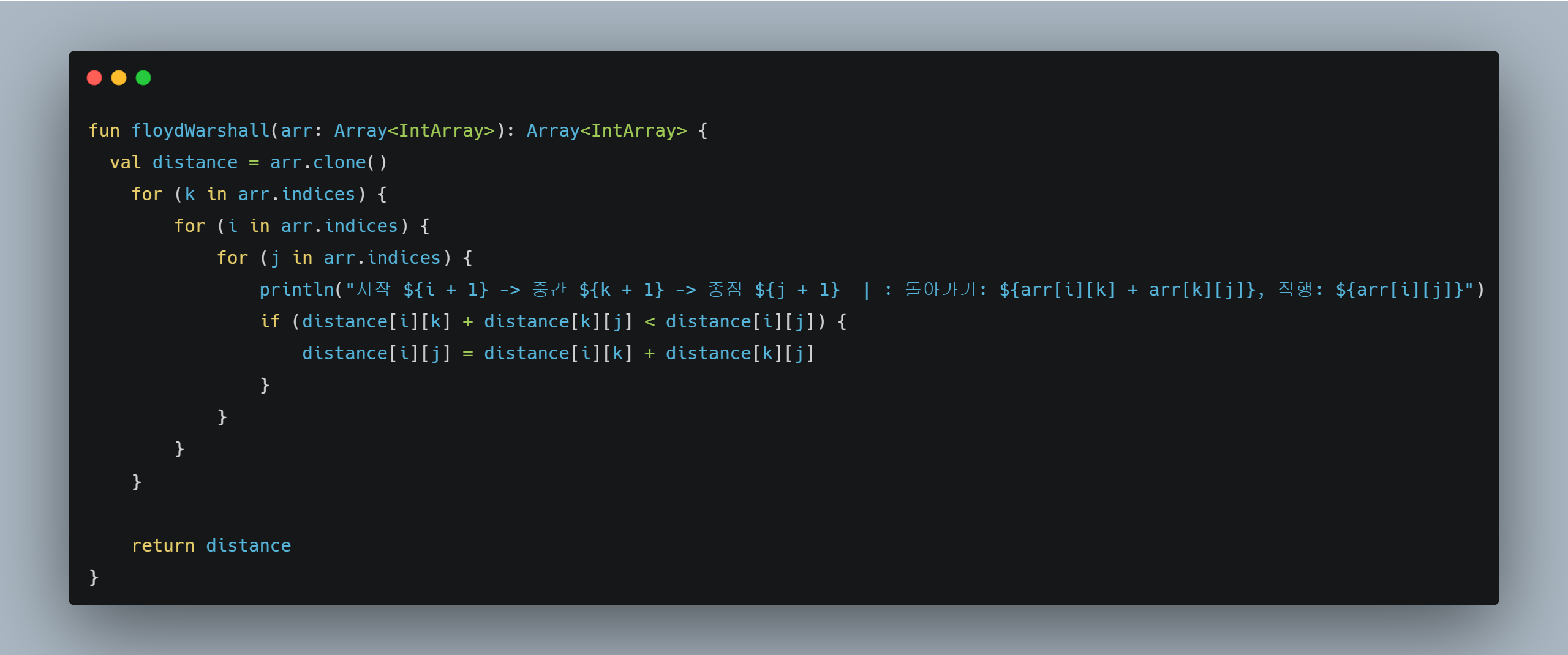
fun floydWarshall(arr: Array<IntArray>): Array<IntArray> {
val distance = arr.clone()
for (k in arr.indices) {
for (i in arr.indices) {
for (j in arr.indices) {
println("시작 ${i + 1} -> 중간 ${k + 1} -> 종점 ${j + 1} | : 돌아가기: ${arr[i][k] + arr[k][j]}, 직행: ${arr[i][j]}")
if (distance[i][k] + distance[k][j] < distance[i][j]) {
distance[i][j] = distance[i][k] + distance[k][j]
}
}
}
}
return distance
}
'알고리즘 > 개념' 카테고리의 다른 글
| BackTracking 백트래킹 설명 및 문제 예시 (0) | 2023.03.14 |
|---|---|
| 다익스트라(Dijkstra) 알고리즘 - Kotlin (0) | 2023.03.07 |
| DFS & BFS ( Kotlin ) (0) | 2023.03.07 |
| 이분탐색 파라매트릭 서치 알고리즘 ( Kotlin ) (0) | 2023.03.07 |
| 크루스칼 알고리즘 & Union Find 알고리즘 ( 최소 신장 트리 , Kotlin ) (0) | 2023.03.02 |