2023. 5. 3. 02:55ㆍ알고리즘/개념
정렬 알고리즘
이번 시간에는 정렬 알고리즘 6개에 대해 설명과 시간복잡도, 그림, 구현 코드를 정리하고 손코딩으로 꼭 외울 수 있게 암기하는 시간을 가져보겠습니다.
아래 참고 사이트
https://www.toptal.com/developers/sorting-algorithms
Sorting Algorithms Animations
Animation, code, analysis, and discussion of 8 sorting algorithms on 4 initial conditions.
www.toptal.com
https://visualgo.net/en/sorting
Sorting (Bubble, Selection, Insertion, Merge, Quick, Counting, Radix) - VisuAlgo
VisuAlgo is generously offered at no cost to the global Computer Science community. If you appreciate VisuAlgo, we kindly request that you spread the word about its existence to fellow Computer Science students and instructors. You can share VisuAlgo throu
visualgo.net
공통 swap extension 함수 아래에 swap 함수는 이거입니다. 또한 아래에 나오는 코드들은 매개변수로 받는 원형 함수를 변형하기 때문에 변형 없이 정렬된 배열을 return 값으로 반환하셔도 됩니다.

1. 삽입 정렬(Insertion Sort)
삽입 정렬은 카드를 정렬하는 방법과 유사합니다. 손 안에 정렬된 카드가 있고 카드를 새로 받을 때마다 올바른 자리를 찾아서 삽입하는 과정입니다.

최선: O(n) 평균: O(n^2) 최악: O(n^2)
삽입 정렬의 구현 과정을 보면 1번 인덱스부터 앞의 인덱스를 확인하며 앞보다 작으면 값을 하나씩 swap 하면서 정렬합니다.
1번부터 0번보다 작으면 1번은 0번 값으로 0번의 값은 1번으로 옮깁니다.
2번부터 1번보다 작으면 2번은 1번 값으로 1번은 2번 값으로 옮깁니다. 다시 1번 값을 기준으로 0번 값을 봅니다. 만약에 값이 크면 멈추고 작으면 다시 1번 값이랑 0번 값을 swap 하고 기준 index값을 -- 합니다. 그러면 index가 0보다 작으니까 반복을 멈추고 다음 i 값으로 갑니다.

fun insertionSort(arr: IntArray) {
for(i in 1 until arr.size) {
var index = i
while(index > 0 && arr[index-1] > arr[index]) {
arr.swap(index, index-1)
index--
}
}
}
2. 선택 정렬 ( Selection Sort )
선택정렬의 기본 방식은 간단하게 생각하면 맨 앞에부터 작은 값을 찾아서 정렬합니다. 맨 앞부터 뒤로 가면서 값이 제일 작은 걸 찾아서 정렬하기 때문에 for문은 맨 앞을 반복하는 거 1개, 뒤로 가면서 작은 값을 찾는 for문 1개로 총 2개의 반복문이 필요하며 시간 복잡도는 항상 O(n^2)가 됩니다. 가장 작은 값의 index를 기억하는 변수를 두어야 뒤로 가면서 작은 값을 비교합니다.

최선 : $$O(n^2)$$ 평균 : $$O(n^2)$$ 최악 : $$O(n^2)$$
코드

fun selectionSort(arr: IntArray) {
for(i in 0 until arr.size-1) {
var minIndex = i
for(j in i+1 until arr.size) {
if(arr[j] < arr[minIndex]) minIndex = j
}
arr.swap(i , minIndex)
}
}3. 버블 정렬 (Bubble Sort)
버블 정렬은 인접한 2개의 레코드를 비교하여 크기가 순서대로 되어 있지 않으면 서로 교환하는 방법입니다. 이러한 비교-교환 과정은 리스트의 왼쪽 끝에서 시작하여 오른쪽 끝까지 진행합니다. 비교-교환 과정이 완료되면 가장 큰 레코드가 리스트의 오른쪽 끝으로 이동합니다. 이 모습이 마치 거품이 보글보글 떠오르는 것과 유사하여 버블 정렬이라고 부릅니다.
최선: O(n^2) 평균: O(n^2) 최악: O(n^2)

코드

fun bubbleSort(arr: IntArray) {
for(i in 0 until arr.size) {
for(j in 1..arr.size-i) {
if(arr[j-1] > arr[j]) arr.swap(j-1, j)
}
}
}
최적화
버블 정렬을 최적화 할 수 있는 방법은 크게 두 가지가 있습니다.
1. 이미 정렬이 완료 되었다면 for문을 탈출하여 필요 없는 연산 x
2. 일부분 정렬된 곳이 있다면 마지막 swap index까지 연산
fun bubbleSort(arr: IntArray): IntArray {
val sortedArr = arr.clone()
var end = sortedArr.size - 1
while (end > 0) {
var lastI = 0
var flag = false
for (index in 1..end) {
if (sortedArr[index - 1] > sortedArr[index]) {
sortedArr.swap(index, index - 1)
flag = true
lastI = i
}
}
if (!flag) break
end = lastI
}
return sortedArr
}중간에 flag가 1번의 경우를 하지 않는 것이고 2번은 일부분 정렬된 곳을 위해 last Index를 저장해 어디까지만 반복할지 정할 수 있습니다. 마지막으로 버블 정렬을 한 곳을 기억하면 다음번 정렬에 그 이후로는 정렬할 필요가 없기 때문에 lastI의 값을 end 값에 저장하여 반복합니다.
4. 쉘 정렬
쉘 정렬은 삽입 정렬이 어느 정도 정렬된 배열에 대해서는 대단히 빠른 것에 착안했습니다. 쉘 정렬은 전체 리스트를 한 번에 정렬하지 않습니다. 일정한 기준에 따라 분류에 연속적이지 않은 여러 개의 부분으로 나누고, 각 부분 배열 혹은 리스트를 삽입 정렬을 이용하여 정렬합니다. 각 부분의 개수가 1이 될 때까지 이 과정을 반복합니다.
실험적 연구를 통하여 셸 정렬의 시간 복잡도는 최선의 경우 정렬이 되어 있는 상태로 O(n), 최악의 경우 O(n^2)이지만 평균적인 경우에는 O(n^1.5)인 것으로 알려져 있습니다.
| 0(j-gap , j) | 1 | 2 | 3 | 4 | 5 (i, j) | 6 | 7 | 8 |
| 5 | 3 | 8 | 4 | 9 | 1 | 6 | 2 | 7 |
| 5 | 1 | |||||||
| 3 | 6 | |||||||
| 8 | 2 | |||||||
| 4 | 7 | |||||||
| 9 | ||||||||
| 1 | 3 | 2 | 4 | 9 | 5 | 6 | 8 | 7 |
간격 : 3
| 1 | 3 | 2 | 4 | 9 | 5 | 6 | 8 | 7 |
| 1 | 4 | 6 | ||||||
| 3 | 9 | 8 | ||||||
| 2 | 5 | 7 | ||||||
| 1 | 3 | 2 | 4 | 8 | 5 | 6 | 9 | 7 |
그리고 간격이 1일 때를 하여 마무리를 합니다.
코드를 보겠습니다.
쉘 정렬의 처음 gap은 보통 전체 배열의 절반 값을 잡고 시작합니다. 그리고 짝수이면 +1을 하기도 하지만 여기서는 그냥 진행하겠습니다. 처음 gap을 절반의 값으로 설정한 뒤에 while문을 진입합니다. 그리고 gap의 값부터 배열의 끝까지 순차적으로 반복합니다. 그리고 제일 안 쪽에 while문의 조건을 보면 j가 gap보다 크거나 같아야 하고 arr [j-gap] 값이 arr [j] 값보다 크면 교환합니다.
예를 들어보면,
i: 0 1 2 3 4 5 6 7 8
arr: 5 3 8 4 9 1 6 2 7
처음 gap = 5이고 5부터 위로 하나씩 올라가면서 gap만큼 아래 값과 비교하면서 갑니다.
5부터 하나씩 올라가는게 가운데 for문이고 gap만큼 계속 아래와 비교-교환하는 게 가장 안 쪽 while문입니다.
처음 5에서 5-5=0의 값과 비교합니다. index 5일 때는 1이고 0일 때는 5입니다. while문 안에 조건문인 아래 값이 위에 값보다 크다가 성립하므로 둘을 자리 교환합니다. 이제 j값을 0으로 바꾸고 다시 아래로 가보지만 0-5는 음수이므로 해당하지 않아 while문을 들어가지 않고 for문의 i값을 증가합니다. 이제 index 6에서 다시 아래 gap 5만큼 아래 있는 index를 확인합니다. index 6 , 1의 값은 각각 6 3입니다. 아래 값이 작으므로 확인하지 않고 다음 아래값은 음수이므로 다시 for문 i를 증가합니다. 이렇게 for문을 끝까지 돌면 gap이 5일 때의 경우가 끝나고 이제 gap /= 2를 하여 gap 값을 2로 만듭니다.
다시 가장 밖의 while문을 확인하고 조건 gap은 현재 2 > 0 이므로 진행합니다. gap = 2 일 때 2부터 갑니다 2 , 0 비교 그리고 3 , 1 비교 4, 2 ,0 드디어 3개를 비교합니다. 계속 비교-교환합니다. 이렇게 진행합니다. 이해가 잘 되셨나요...???
fun shellSort(arr: IntArray) {
var gap = arr.size / 2
while (gap > 0) {
for(i in gap until arr.size) {
var j = i
while (j - gap >= 0 && arr[j - gap] > arr[j]) {
arr.swap(j-gap, j)
j -= gap
}
}
gap /= 2
}
}
5. 병합 정렬(merge sort)
병합 정렬은 하나의 배열 혹은 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분을 정렬한 다음, 두 리스트를 합하여 전체가 정렬된 리스트로 만드는 방법입니다. 이것은 분할 정복(Divide and Conquer) 기법에 바탕을 두고 있는데, 하나의 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략입니다. 만약 분할된 문제가 아직도 충분히 작지 않아 해결하기 어렵다면, 분할 정복 방법으로 연속해서 다시 적용합니다. 이때 보통 순한 호출을 사용합니다.
병합 정렬은 레코드 개수 n이 2의 거듭제곱이라고 가정하고 순환 호출의 깊이가 얼마나 되는지 알 수 있습니다. 만약 n = 2^3인 경우에는 부분 배열의 크기가 2^3 , 2^2 , 2^1 , 2^0 순으로 줄어들어 순환 호출의 깊이가 3 임을 알 수 있습니다.
병합 정렬의 알고리즘은 다음과 같습니다.
mergeSort(arr, left, right)
if left < right
mid =(left+right)/2
mergeSort(arr, left, mid)
mergeSort(arr, mid+1, right)
merge(arr, left, mid, right)
병합 알고리즘은 다음과 같습니다.
merge(arr, left, mid, right)
i = left
e1 = mid
j = mid+1
e2 = right
sorted 배열
k = 0
while i <= e1 and i <= e2 do
if list [i] < list [j]
then sorted [k++] = arr [i++]
else sorted [k++] = arr [j++]
요소가 남아있는 부분배열을 sorted로 복사
sorted배열을 원 배열에 복사
병합 정렬 코드
fun mergeSort(arr: IntArray, left: Int, right: Int) {
if (left < right) {
val mid = (left + right) / 2
mergeSort(arr, left, mid)
mergeSort(arr, mid + 1, right)
merge(arr, left, mid, right)
}
}
병합 코드
빈 배열이나 리스트를 만들어서 먼저 각 요소들을 크기에 따라 정렬합니다. 그 후에 한쪽이 모두 끝난 경우를 생각해 들어가지 않은 원소들을 정렬 배열에 전부 삽입합니다. 그리고 정렬된 배열 혹은 리스트를 left와 right에 맞게 하나씩 다시 값을 변경합니다. sortedArr = IntArray(arr.size) 이렇게 선언 후에 하셔도 되고 mutableList로 만드셔도 됩니다.
1. arr 방법
fun merge(arr: IntArray, left: Int, mid: Int, right: Int) {
var i = left
var j = mid + 1
val sortedArr = IntArray(arr.size)
var k = left
while (i <= mid && j <= right) {
sortedArr[k++] = if (arr[i] <= arr[j]) arr[i++] else arr[j++]
}
if (i > mid) {
for (l in j..right) sortedArr[k++] = arr[l]
} else {
for (l in i..mid) sortedArr[k++] = arr[l]
}
for (l in left..right) arr[l] = sortedArr[l]
}
2. mutableList 방법
fun merge(arr: IntArray, left: Int, mid: Int, right: Int) {
var i = left
var j = mid + 1
val sorted = mutableListOf<Int>()
var k = left
while (i <= mid && j <= right) {
sorted.add(if (arr[i] <= arr[j]) arr[i++] else arr[j++])
}
if (i > mid) {
for (l in j..right) sorted.add(arr[l])
} else {
for (l in i..mid) sorted.add(arr[l])
}
for (l in left..right) arr[l] = sorted.removeFirst()
}6. 퀵 정렬
퀵 정렬은 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬 방법입니다. 퀵 정렬도 병합 정렬과 같이 분할-정복법을 사용합니다. 그러나 병합 정렬과는 달리 리스트를 균등하게 분할할 필요가 없습니다.
먼저 배열 or 리스트 안에 있는 한 요소를 피벗으로 선택합니다. 여기서는 배열의 첫 번째 요소를 피벗으로 합니다. 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮기고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮깁니다. 결과적으로 피벗을 중심으로 왼쪽은 피벗보다 작은 요소, 오른쪽은 큰 요소로 구성됩니다. 이 상태에서 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬하게 되면 전체 리스트가 정렬됩니다.
그러면 퀵 정렬은 어떻게 피벗을 기준으로 나누어진 왼쪽 부분 리스트와 오른쪽 부분 리스트를 정렬할까요? 여기에서도 순환 호출이 사용됩니다. 부분 리스트 or 배열에서도 다시 피벗을 정하고 피벗을 기준으로 2개의 부분 배열로 나누는 과정이 되풀이됩니다. 이 과정은 부분 리스트를 더 이상 분할할 수 없을 때까지 반복합니다.
퀵 정렬도 크게 2개로 나누어서 구현합니다. 먼저 퀵 정렬을 분할 정복을 이용하여 구성하는 함수와 피벗을 기준으로 왼쪽과 오른쪽으로 옮겨 정렬하는 partition() 함수로 구성됩니다.
그림을 보시겠습니다.
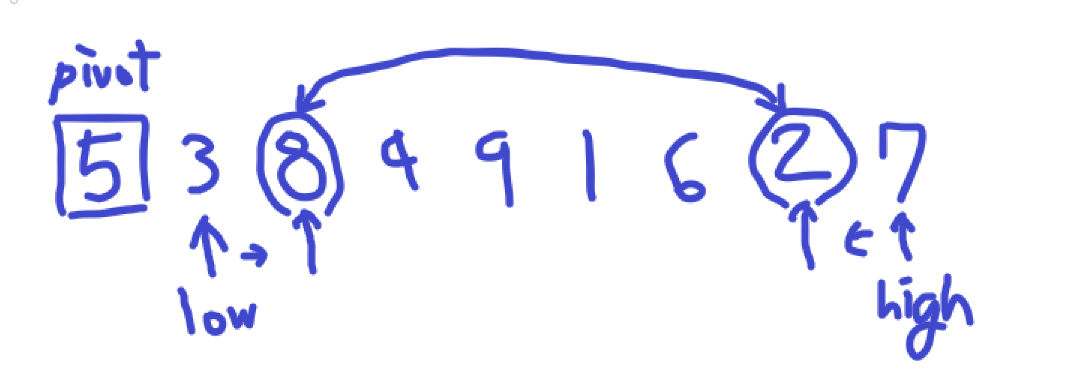
왼쪽에 pivot 5가 있고 left는 index 1입니다. low는 1부터 올라가고 right는 8이고 high는 8부터 내려옵니다.
먼저 low가 올라갑니다. 올라가다가 pivot보다 큰 수 8을 만나면 멈춥니다.
이제 high가 내려옵니다. 내려오다가 pivot보다 작은 수 2를 만나 멈춥니다.
둘을 교환합니다. 그리고 low가 아직 high보다 작기 때문에 다시 반복합니다.
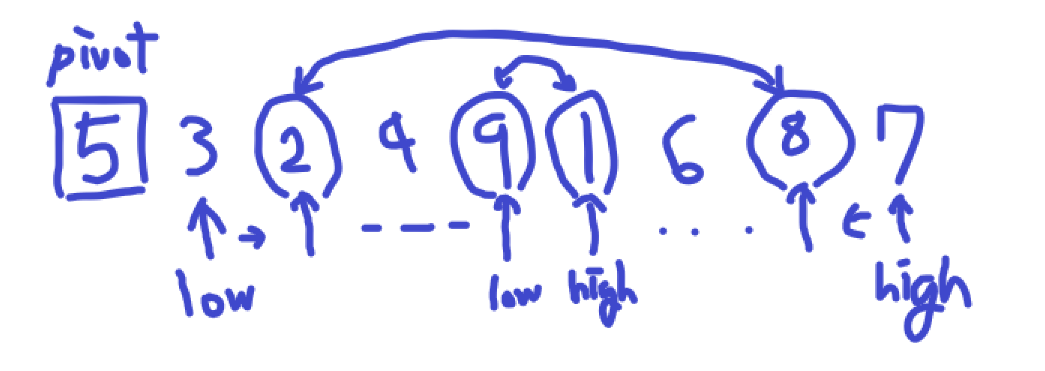
low가 먼저 계속 올라가다가 pivot보다 큰 9를 만나 멈춥니다.
high가 이제 계속 내려오다가 pivot보다 작은 1을 만나 멈춥니다.
9와 1을 교환합니다.
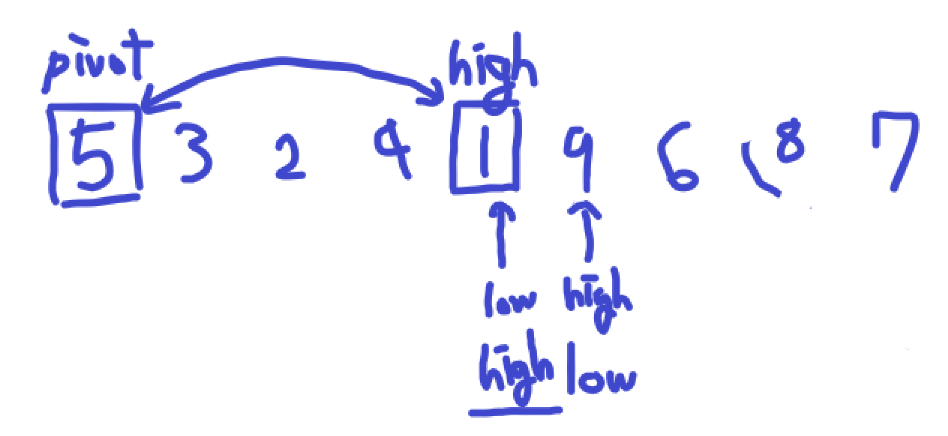
다시 low가 high보다 아직은 작기 때문에 반복합니다.
먼저 low가 올라갑니다. 올라가자마자 pivot보다 큰 값을 만나게 되어 멈춥니다.
이제 high가 내려옵니다. 내려오자마자 pivot보다 작은 값을 만나게 되어 멈춥니다.
하지만 현재 low가 high보다 큰 상태입니다. 그러므로 교환은 일어나지 않고 탈출합니다.
이제 high 인덱스에 있는 값과 pivot의 값을 교환합니다.

1번의 과정이 위의 결과로 끝나게 됩니다. 이제 위의 배열을 가지고 어떻게 해야 할까요?
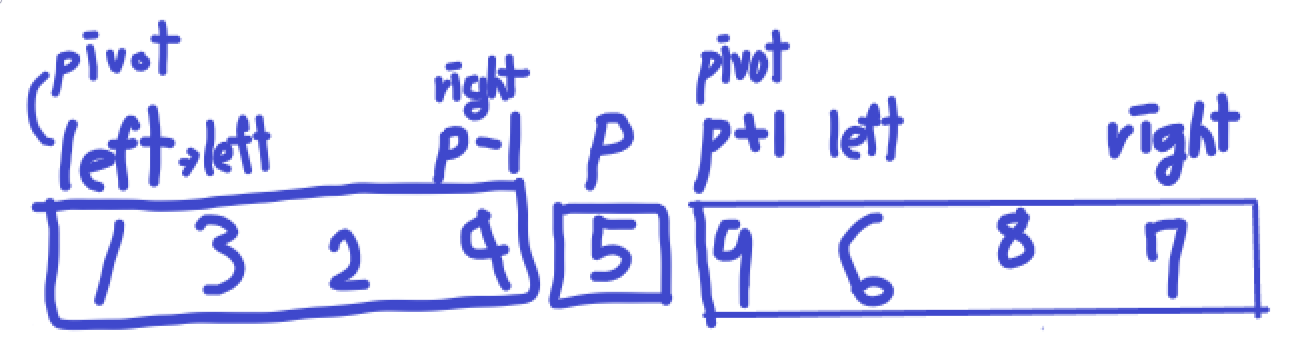
위의 정렬된 배열을 다시 나누어서 quick sort 하게 됩니다. p를 반환받아 high 값을 기준으로 다시 왼쪽, 오른쪽으로 나누어 각각을 위에 과정을 거치게 됩니다. 왼쪽은 1을 pivot으로 잡고 반복합니다. 오른쪽은 9를 pivot으로 잡고 위의 과정을 반복합니다.
최선: O(nlogn) 평균 : O(nlogn) 최악 : O(n^2)
최악의 경우는 잡은 pivot보다 계속 불균형하게 교환이 일어나며 배열을 쪼개 quick sort 하는 것입니다.
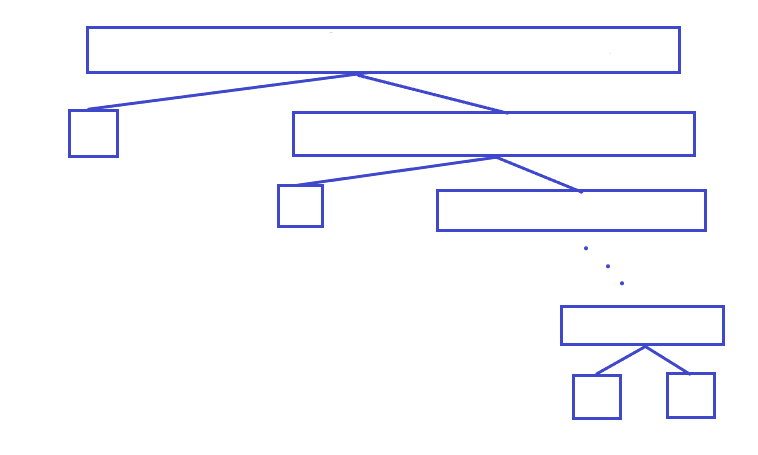
퀵 정렬 함수
fun quickSort(arr: IntArray, left: Int, right: Int) {
if (left < right) {
val q = partition(arr, left, right)
quickSort(arr, left, q - 1)
quickSort(arr, q + 1, right)
}
}
partition 1 함수
fun partition(arr: IntArray, left: Int, right: Int): Int {
var low = left + 1
var high = right
val pivot = arr[left]
while (low <= high) {
while (low <= right && arr[low] < pivot) low++
while (high >= left && arr[high] > pivot) high--
if (low < high) arr.swap(low, high)
}
arr.swap(left, high)
return high
}
partition 2 함수
두 번째는 low와 high를 비교하는 게 아닌 pivot을 똑같이 왼쪽으로 잡고 작은 값만 찾으면서 교환할 자리의 index를 기억해 교환하는 방식입니다.

진행방식을 그림으로 표현해 보겠습니다. 먼저 pivot은 맨 왼쪽입니다. i와 j는 left인 0부터 출발합니다. 이제 j가 left =0부터 right = 8까지 반복합니다. 만약에 pivot값보다 arr [j]에 있는 값이 작으면 i값을 하나 올리고 i자리와 j자리의 값을 swap 합니다. 현재 i와 j의 값은 5이므로 넘어가고 j가 하나 올라갑니다.

j가 하나 올라가네 3의 값을 pivot과 비교합니다. pivot보다 작으므로 i값을 하나 증가시키고 i와 j의 값을 교환합니다. 이때 같은 자리에 있으므로 3 그대로 있습니다.

j가 하나 올라가서 8의 값을 pivot과 비교합니다. 8은 pivot보다 크므로 그냥 넘어갑니다.

j가 하나 올라가서 4의 값을 pivot과 비교합니다. 5보다 작으므로 i를 하나 올리고 i에 있는 값과 j에 있는 값을 교환합니다.
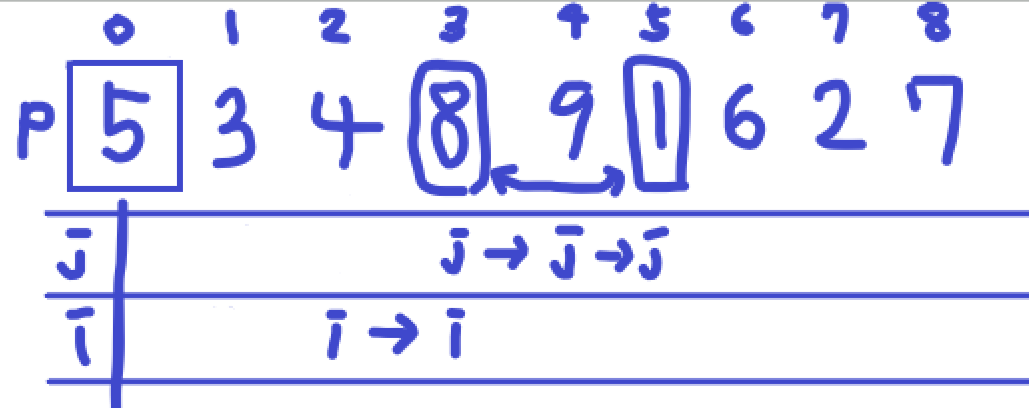
j가 4일 때는 9이므로 넘어가고 5일 때 pivot보다 작으므로 i를 하나 올려 i가 3일 때와 j가 5일 때를 교환합니다.

j는 6일 때는 넘어가고 7일 때 pivot보다 작으므로 i를 하나 올려서 4일 때 값과 교환합니다.
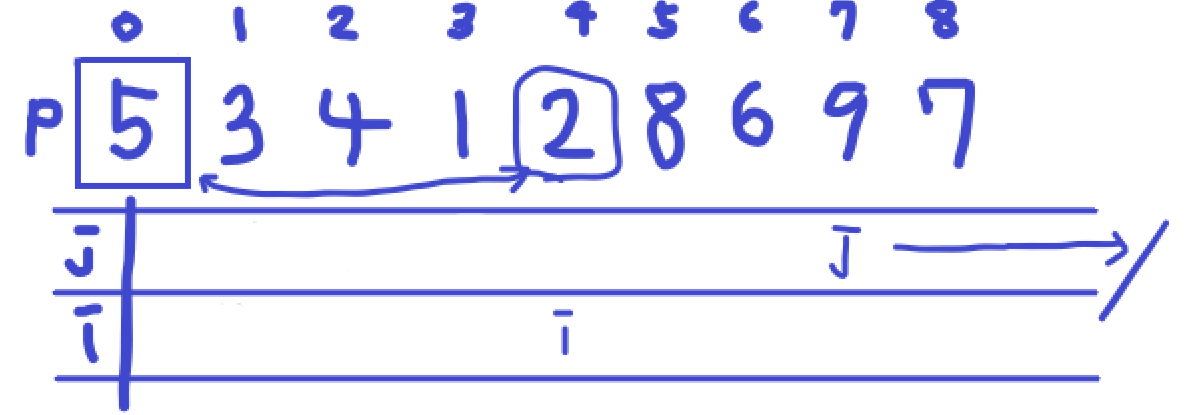
j가 8일 때는 7의 값이므로 넘어가고 이제 반복문이 끝납니다. 그러면 그때의 i 값과 pivotindex 값을 교환합니다.
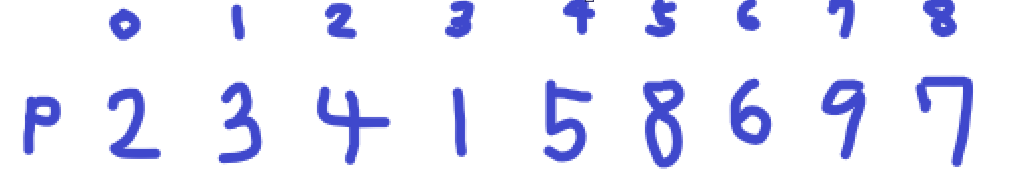
이렇게 첫 번째 partition 함수를 마무리하고 순환 호출로 quick sort를 시작합니다.
코드
fun partition(arr: IntArray, left: Int, right: Int, pivotIndex: Int): Int {
val pivot = arr[pivotIndex]
var i = left
for (j in left..right) {
if (arr[j] < pivot) arr.swap(++i,j)
}
arr.swap(pivotIndex,i)
return i
}
시간 복잡도 정리
| 최고 | 평균 | 최악 | |
| 삽입 Insertion | $$N$$ | $$N^2$$ | $$N^2$$ |
| 선택 Selection | $$N^2$$ | $$N^2$$ | $$N^2$$ |
| 버블 Bubble | $$N^2$$ | $$N^2$$ | $$N^2$$ |
| 쉘 Shell | $$N$$ | $$N^{1.5}$$ | $$N^2$$ |
| 병합 Merge | $$NlogN$$ | $$NlogN$$ | $$NlogN$$ |
| 퀵 Quick | $$NlogN$$ | $$NlogN$$ | $$N^2$$ |
이렇게 6가지 정렬에 대해 알아보았습니다. 부족한 부분도 많지만 그래도 함께 암기하고 공부할 수 있으면 좋겠습니다. 도움이 되길 바라면서 이만 마치겠습니다. 감사합니다!
'알고리즘 > 개념' 카테고리의 다른 글
| Prim Algorithm kotlin (0) | 2023.06.21 |
|---|---|
| BackTracking 백트래킹 설명 및 문제 예시 (0) | 2023.03.14 |
| 다익스트라(Dijkstra) 알고리즘 - Kotlin (0) | 2023.03.07 |
| DFS & BFS ( Kotlin ) (0) | 2023.03.07 |
| 이분탐색 파라매트릭 서치 알고리즘 ( Kotlin ) (0) | 2023.03.07 |