2023. 3. 14. 22:09ㆍ알고리즘/개념
백트래킹이 무엇인가요??
백트래킹 기법은 해를 찾는 중에 어떤 시점에서 해가 될 수 없다 판단되면 가능했던 시점까지 돌아가 다른 경우로 다시 탐색하는 과정이라고 합니다.
백트래킹은 왜 사용하나요??
백트래킹은 모든 경우를 따져볼 때 사용하기 좋습니다. 대표적으로 dfs와 함께 사용하는데 모든 경우를 깊이 탐색하면 각 노드를 확인할 때 백트래킹으로 불가능한 시점을 탐색하지 않고 다음 경우로 넘길 수 있어 효율적으로 모든 경우를 탐색 가능하게 합니다.
백트래킹은 어떻게 구현하나요??
N-Queen 문제
출처: 프로그래머스
https://school.programmers.co.kr/learn/courses/30/lessons/12952
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
이 포스트는 광고 게시가 없는 비상업적, 비영리적 포스트임을 알려드립니다.
N - Queen 문제는 대표적인 BackTracking 문제입니다.

먼저 그냥 dfs로 풀 때를 생각해 보겠습니다.
아래에 판이 있습니다.
첫 번째 Q를 넣는다면 아래처럼 하나씩 처음부터 끝까지 넣을 수 있습니다.


하지만 두 번째 Q를 넣게 되면
아래 그림처럼 중복되는 경우가 발생합니다.


이렇게 가능하면서 중복까지 전부 탐색하게 되면 1번의 q를 16번 하게 되고 다음 q를 넣기 위해 1개의 경우가 다시 16이 되므로 16의 16승이 되게 됩니다.
이렇게 될 경우 너무 큰 시간 복잡도를 갖게 됩니다. 비효율적이죠.
이제 백트래킹을 이용하여 풀어보겠습니다.
백트래킹을 다시 말하면
백트래킹 기법은 해를 찾는 중에 " 어떤 시점에서 해가 될 수 없다 판단되면 가능했던 시점까지 돌아가 다른 경우로 다시 탐색 " 하는 과정이라고 합니다.
백트래킹을 위해 어떤 시점에서 해가 될 수 없다는 걸 알려주어야 합니다.
N Queen에서는 어떤 경우일까요??
아래에 그림이 있습니다.
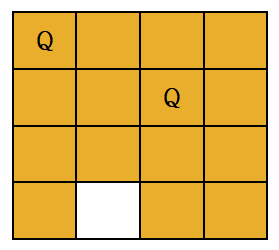
Q가 0,0에 있다고 하면 가로 세로 대각선은 가능하지 못합니다.



만약 Q가 위 가운데 그림처럼 색이 칠해진 칸에 들어가게 되면 현재 시점의 탐색은 불가능하다 판단하고 다시 가능했던 시점까지 되돌아가고 그 이후에 다시 탐색합니다. 마지막 사진이 다시 탐색하는 경우 가능하므로 행이 하나 내려가게 됩니다.
세 번째 행을 탐색할 때 아래 그림은 가능한 영역을 보여주고 있습니다.
세 번째 행에는 가능한 곳이 없기 때문에 되돌아갑니다. 되돌아간 후 다시 Q를 하나 올려서 확인하는데 가능하므로 내려갑니다.
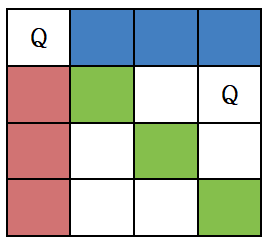
이렇게 계속 확인하고 가능한 영역까지 되돌아가고 이러한 과정을 백트래킹이라고 합니다.
코드
첫 번째
첫 번째는 가로 세로 대각선의 확인을 HashSet을 이용한 방법입니다.
class SolutionNQueen {
val colCheckHash = HashSetOf<Int>()
val xyMinus = HashSetOf<Int>()
val xySum = HashSetOf<Int>()
fun solution(n: Int): Int = backTracking(n = n, row = 0, count = 0)
fun backTracking(n: Int, row: Int, count: Int): Int {
var cnt = count
if (row == n) return cnt + 1
else {
for (column in 0 until n) {
if (!colCheckHash.contains(column)
&& !xyMinus.contains(row - column)
&& !xySum.contains(row + column)
) {
colCheckHash.add(column)
xyMinus.add(row-column)
xySum.add(row+column)
cnt = backTracking(n, row+1, cnt)
colCheckHash.remove(column)
xyMinus.remove(row - column)
xySum.remove(row + column)
}
}
}
return cnt
}
}
두 번째
두 번째 풀이는 가로 세로 대각선의 확인을 배열 + for문을 이용한 방법입니다.
class SolutionNQueen {
lateinit var colArr: IntArray
fun solution(n: Int): Int {
colArr = IntArray(n) { -1 }
return backTracking(n = n, row = 0, count = 0)
}
fun backTracking(n: Int, row: Int, count: Int): Int {
var cnt = count
if (row == n) return cnt + 1
else {
for (column in 0 until n) {
if (check(row, column)) {
colArr[row] = column
cnt = backTracking(n, row + 1, cnt)
colArr[row] = -1
}
}
}
return cnt
}
fun check(row: Int, column: Int): Boolean {
for (k in 0 until row) {
if (colArr[row] == column || abs(colArr[k] - column) == abs(k - row))
return false
}
return true
}
}
'알고리즘 > 개념' 카테고리의 다른 글
| Prim Algorithm kotlin (0) | 2023.06.21 |
|---|---|
| 정렬 알고리즘 정리 코틀린 (0) | 2023.05.03 |
| 다익스트라(Dijkstra) 알고리즘 - Kotlin (0) | 2023.03.07 |
| DFS & BFS ( Kotlin ) (0) | 2023.03.07 |
| 이분탐색 파라매트릭 서치 알고리즘 ( Kotlin ) (0) | 2023.03.07 |