2023. 6. 21. 20:20ㆍ알고리즘/개념
Prim Algorithm
특징
- 무향 그래프에 적용 가능
- 모든 꼭지점을 포함하는 최소 신장 트리를 알 수 있다. ( MST )
개념
0-4까지 5개의 노드가 있고 아주 특별한 주머니가 하나 있다. 이 주머니는 안에 들어있는 값들 중 가장 작은 값을 뱉는다. 이제 정점들을 모두 포함하고 가중치의 합이 가장 작은 신장 트리를 Prim Algorithm을 이용해 구해보자.
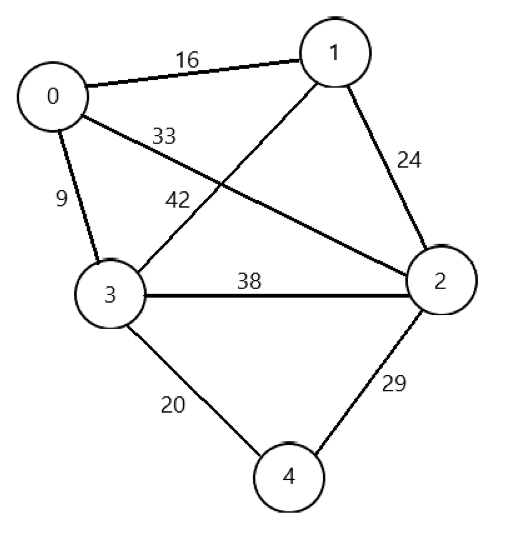
아무 노드 하나를 골라보자. 2번을 선택하자. 2번 정점을 이제 주머니에 넣자.
현재 거리 합계 : 0
방문 상황: 0 -> 미방문 , 1 -> 방문
0번 0
1번 0
2번 0
3번 0
4번 0
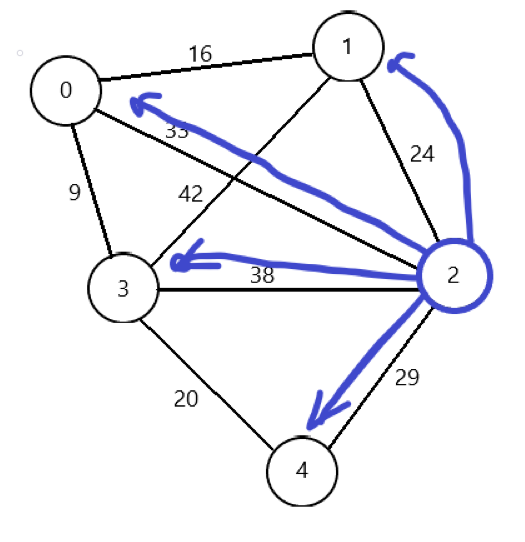
특별한 주머니에서 하나 꺼내보니 방금 넣었던 2번 정점이 들어있다. 이제 2번 정점으로 가자. 2번 정점은 방문 처리를 한다. 2번이 시작 거리이므로 거리 합계가 없다. 2번에서는 0,1,3,4번 노드에 갈 수 있다. 갈 수 있는 0,1,3,4 정점을 특별한 주머니에 넣는다.
현재 거리 합계 : 0
방문 상황: 0 -> 미방문 , 1 -> 방문
0번 0
1번 0
2번 1
3번 0
4번 0
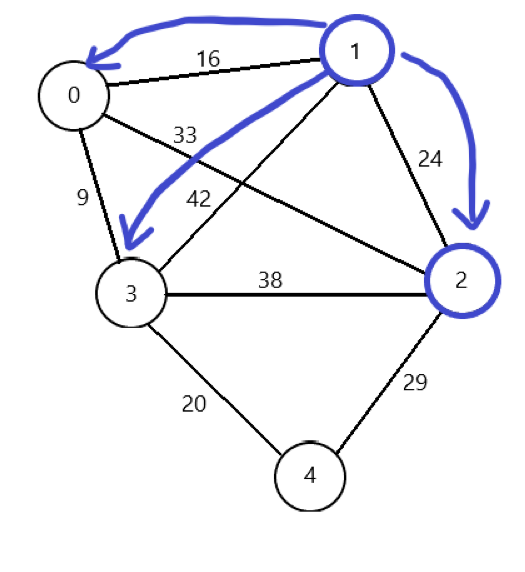
특별한 주머니에서 하나 꺼내보자. 하나 꺼내보니 1번이 나왔다. 1번을 방문 처리하고 2번에서 1번으로 가는 24 가중치를 거리 합계에 더해준다. 그리고 1번에서 갈 수 있는 정점들을 확인해보자. 1번은 0,2,3에 갈 수 있다. But 2번은 방문했었으니 0,3번을 주머니에 넣자.
현재 거리 합계 : 24
방문 상황: 0 -> 미방문 , 1 -> 방문
0번 0
1번 1
2번 1
3번 0
4번 0
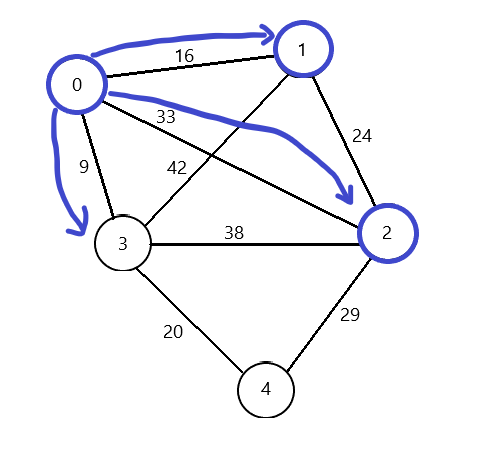
또 주머니에서 하나 꺼내보자. 0번이 나왔다. 0번으로 가고 방문처리와 0번으로 가는 16 거리를 거리 합계에 더해준다.
0번에서 갈 수 있는 정점들은 1,2,3이 있다. 1,2는 이미 방문 했던 적이 있으므로 갈 수 있는 3번 정정을 특별한 주머니에 넣는다.
현재 거리 합계 : 24 + 16
방문 상황: 0 -> 미방문 , 1 -> 방문
0번 1
1번 1
2번 1
3번 0
4번 0
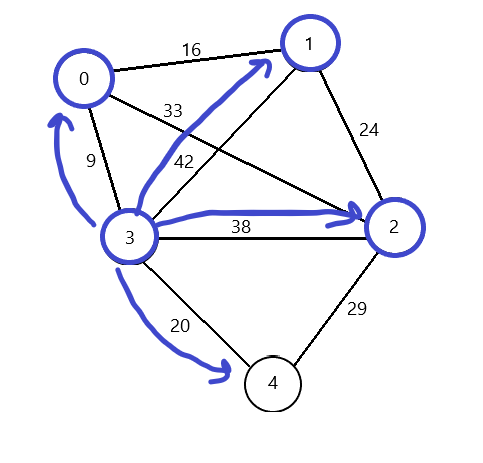
주머니에서 하나 또 꺼내본다. 3번이 나왔다. 3번을 방문하고 3번까지 거리를 거리 합계에 더한다. 3번은 4개의 정점 0,1,2,4로 갈 수 있다. 하지만 0,1,2는 방문했었으므로 4번만 주머니에 넣는다.
현재 거리 합계 : 24 + 16 + 9
방문 상황: 0 -> 미방문 , 1 -> 방문
0번 1
1번 1
2번 1
3번 1
4번 0
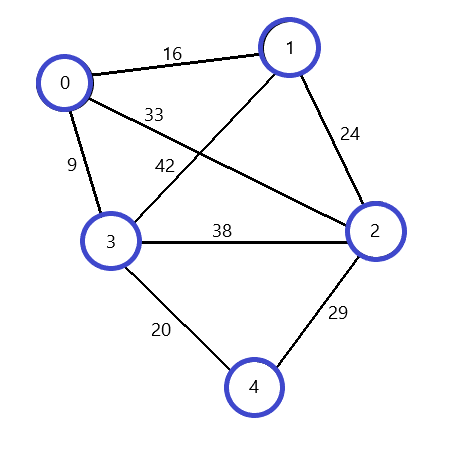
주머니에서 하나 꺼내보자. 4번 정점이 나왔다. 4번 정점을 방문 처리하고 3번에서 4번으로 가는 가중치 20을 거리 합계에 더한다. 4번에서는 2,3을 갈 수 있지만 둘 다 방문 했으므로 주머니에 넣지 않는다.
현재 거리 합계 : 24 + 16 + 9 + 20
방문 상황: 0 -> 미방문 , 1 -> 방문
0번 1
1번 1
2번 1
3번 1
4번 1
다시 주머니를 확인한다. 들어있긴한데 방문했던것들만 남았다. 전부 필요없기 때문에 주머니를 비우고 위의 과정을 끝마친다.
결과를 보면 모든 정점을 전부 다 방문했고 거리 합계는 69이다. 현재 방문한 길은 아래와 같다.
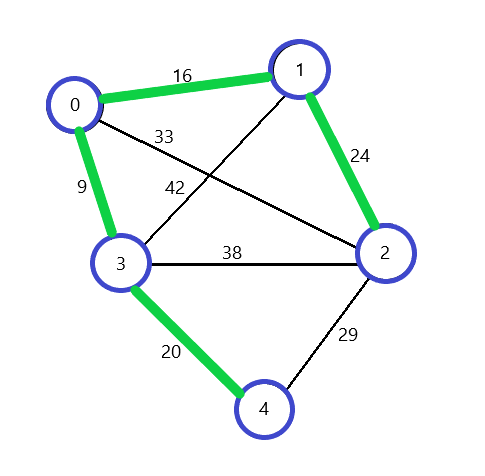
이렇게 최소 신장 트리가 완성되었다. 위와 같은 방법으로 최소 신장 트리 MST를 구하는 방식을 프림 알고리즘이라고 한다.
코드
특별한 주머니 = 우선순위 큐
Prim 함수
fun prim(start: Int, arr: Array<Array<Pair<Int, Int>>>) : Int {
var result = 0
val visited = IntArray(arr.size) { 0 }
val pQueue = PriorityQueue<Pair<Int,Int>> { p1, p2 ->
p1.second.compareTo(p2.second)
}
pQueue.add(Pair(start, 0))
while(pQueue.isNotEmpty()) {
val current = pQueue.poll()
if(visited[current.first] != 1) {
visited[current.first] = 1
result += current.second
arr[current.first].forEach { next ->
if(visited[next.first] != 1) pQueue.add(next)
}
}
}
return result
}Main 함수
fun main(args: Array<String>) {
val graph = arrayOf(
arrayOf(Pair(1, 16), Pair(2, 33), Pair(3, 9)),
arrayOf(Pair(0, 16), Pair(2, 24), Pair(3, 42)),
arrayOf(Pair(0, 33), Pair(1, 24), Pair(3, 38), Pair(4, 29)),
arrayOf(Pair(0, 9), Pair(1, 42), Pair(2, 38), Pair(4, 20)),
arrayOf(Pair(2, 29), Pair(3, 20)),
)
println(prim(2,graph))
}'알고리즘 > 개념' 카테고리의 다른 글
| 정렬 알고리즘 정리 코틀린 (0) | 2023.05.03 |
|---|---|
| BackTracking 백트래킹 설명 및 문제 예시 (0) | 2023.03.14 |
| 다익스트라(Dijkstra) 알고리즘 - Kotlin (0) | 2023.03.07 |
| DFS & BFS ( Kotlin ) (0) | 2023.03.07 |
| 이분탐색 파라매트릭 서치 알고리즘 ( Kotlin ) (0) | 2023.03.07 |